Any advertisements appearing above this line are inserted by "tripod", please IGNORE them
Solomon's kiyyors ("basins")
by Prof. Mordochai ben-Tziyyon, Universitah Ha'ivrit, Y'rushalayim
In addition to the "Sea", Solomon also made ten large copper כִּיֹּרוֹת kiyyorot ("basins") and ten wheeled מְכֹנוֹת m'chonot (literally, "machines") to support them (M'lachim Alef 7:27-38). According to Divrei ha-Yamim Beit 4:6, these kiyyors were used for rinsing the sacrificial flesh of offerings that were to be burned on the Great Altar after the animals had been flayed (i.e. skinned) and dismembered.
The description of the basins is terse:
| וַיַּעַשׂ עֲשָׂרָה כִּיֹּרוֹת נְחֹשֶׁת אַרְבָּעִים בַּת יָכִיל הַכִּיּוֹר הָאֶחָד אַרְבַּע בָּאַמָּה הַכִּיּוֹר הָאֶחָד כִּיּוֹר אֶחָד עַל-הַמְּכוֹנָה הָאַחַת לְעֶשֶׂר הַמְּכֹנוֹת. | Then he made ten copper kiyyors---each kiyyor could hold forty bats [of water] and each kiyyor was four ammahs [across]... there was one kiyyor for each of the ten m'chonot. (M'lachim Alef 7:38) |
The m'chonot that the kiyyors stood on, however, are described in minute detail:
| וַיַּעַשׂ אֶת-הַמְּכֹנוֹת עֶשֶׂר נְחֹשֶׁת אַרְבַּע בָּאַמָּה אֹרֶךְ הַמְּכוֹנָה הָאֶחָת וְאַרְבַּע בָּאַמָּה רָחְבָּהּ וְשָׁלֹשׁ בָּאַמָּה קוֹמָתָהּ. וְזֶה מַעֲשֵׂה הַמְּכוֹנָה מִסְגְּרֹת לָהֶם וּמִסְגְּרֹת בֵּין הַשְׁלַבִּים. וְעַל-הַמִּסְגְּרוֹת אֲשֶׁר בֵּין הַשְׁלַבִּים אֲרָיוֹת בָּקָר וּכְרוּבִים וְעַל-הַשְׁלַבִּים כֵּן מִמָּעַל וּמִתַּחַת לַאֲרָיוֹת וְלַבָּקָר לֹיוֹת מַעֲשֵׂה מוֹרָד. וְאַרְבָּעָה אוֹפַנֵּי נְחֹשֶׁת לַמְּכוֹנָה הָאַחַת וְסַרְנֵי נְחֹשֶׁת וְאַרְבָּעָה פַעֲמֹתָיו כְּתֵפֹת לָהֶם מִתַּחַת לַכִּיֹּר הַכְּתֵפֹת יְצֻקוֹת מֵעֵבֶר אִישׁ לֹיוֹת. וּפִיהוּ מִבֵּית לַכֹּתֶרֶת וָמַעְלָה בָּאַמָּה וּפִיהָ עָגֹל מַעֲשֵׂה-כֵן אַמָּה וַחֲצִי הָאַמָּה וְגַם-עַל-פִּיהָ מִקְלָעוֹת וּמִסְגְּרֹתֵיהֶם מְרֻבָּעוֹת לֹא-עֲגֻלּוֹת. וְאַרְבַּעַת הָאוֹפַנִּים לְמִתַּחַת לַמִּסְגְּרוֹת וִידוֹת הָאוֹפַנִּים בַּמְּכוֹנָה וְקוֹמַת הָאוֹפַן הָאֶחָד אַמָּה וַחֲצִי הָאַמָּה. וּמַעֲשֵׂה הָאוֹפַנִּים כְּמַעֲשֵׂה אוֹפַן הַמֶּרְכָּבָה יְדוֹתָם וְגַבֵּיהֶם וְחִשֻּׁקֵיהֶם וְחִשֻּׁרֵיהֶם הַכֹּל מוּצָק. וְאַרְבַּע כְּתֵפוֹת אֶל אַרְבַּע פִּנּוֹת הַמְּכֹנָה הָאֶחָת מִן-הַמְּכֹנָה כְּתֵפֶיהָ. וּבְרֹאשׁ הַמְּכוֹנָה חֲצִי הָאַמָּה קוֹמָה עָגֹל סָבִיב וְעַל רֹאשׁ הַמְּכֹנָה יְדֹתֶיהָ וּמִסְגְּרֹתֶיהָ מִמֶּנָּה. וַיְפַתַּח עַל-הַלֻּחֹת יְדֹתֶיהָ וְעַל מִסְגְּרֹתֶיהָ כְּרוּבִים אֲרָיוֹת וְתִמֹרֹת כְּמַעַר-אִישׁ וְלֹיוֹת סָבִיב. כָּזֹאת עָשָׂה אֵת עֶשֶׂר הַמְּכֹנוֹת מוּצָק אֶחָד מִדָּה אַחַת קֶצֶב אֶחָד לְכֻלָהְנָה. | He made the ten copper m'chonot---each m'chonah was four ammahs long, four ammahs wide, and three ammahs high. The construction of each m'chonah was as follows. They had frames, and cross-members between the struts. On the cross-members between the struts were [decorative] lions, cattle, and k'ruvim. There was a base on top of the struts, and hammered metal filigree below the lions and the cattle. Each m'chonah had four copper wheels and copper axles, and the four corners had ledges [lit. "shoulders"]; the ledges were cast below the kiyyor, adjacent to the filigree. Its opening was within the top [extending] one ammah upwards; the mouth was round, constructed in the same fashion as the base, one and a half ammahs [across]. There were engravings on the mouth, too, and the frames were square rather than circular. The four wheels were [mounted] at the bottom of the framework and the axle-sockets were built into the base: [the hub of] each wheel was [mounted] one and a half ammahs high [above the ground]. The wheels were fashioned like a chariot-wheel: their axles, hubs, rims and spokes were all of cast [metal]. Each m'chonah had four ledges, [one] at [each of] its four corners: these ledges were part of the m'chonah. One the top of the m'chonah was a round crown half an ammah high enclosing the opening, and the struts and framework of the top were all part of the main structure. He engraved k'ruvim, lions and palm-trees on the metal sheeting, the struts and framework; [they were all firmly] attached, and decorated with filigree. He made all the ten m'chonot in the same way; they were all cast at the same time, of the same size, and in the same design. (M'lachim Alef 7:27-37) |
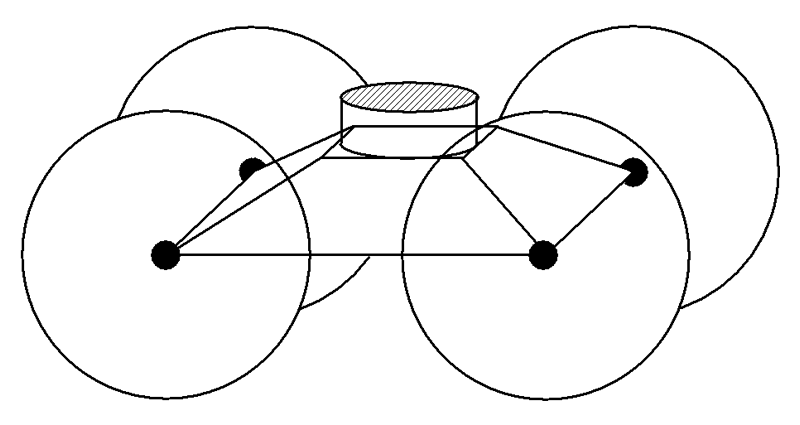
Put simply, each m'chonah ("machine") consisted of a square framework one ammah (about 50cm or 1ft.7½in.) high, measuring four ammahs by four ammahs (2m or 6ft.6¾in. square) at the base and rising to a square top measuring 1½ ammahs by 1½ ammahs (75cm or 2ft.5½in. square) at the top, one ammah (50cm or 1ft.7½in.) above the base, crowned by a circular cylinder 1½ ammahs across and half an ammah (25cm or 9¾in.) high, open at the top to support the kiyyor ("basin"). At each corner was a pair of wheels each three ammahs (150cm or 4ft.11in.) in diameter. The whole contraption therefore stood three ammahs (150cm or 4ft.11in.) high, and would have looked something like Figure 1:
 |
| Figure 1: M'chonah ("machine") for supporting a kiyyor ("basin") |
About the shape of the kiyyors we are told nothing, although it is logical to conclude that they were round because they were supported on the 1½-ammah-wide hollow cylinders that rose from the crowns of the m'chonot. One thing is sure: they were BIG---four ammahs or two metres (about 6½ feet) across---and held a LOT of water---40 bats, equal to about 1,125 litres or approx. 250 imperial gallons (300 American gallons). This enormous quantity of water would have weighed a staggering 1,125kg or 1.125 metric tonnes (just over one imperial ton or 1¼ American "short tons")!
It is interesting to speculate about the possible shape of the kiyyors. We know that they were round and had a diameter of 4 ammahs at their brims, and held 40 bats of water. Now 1 bat is equal to 3 sé'ahs and 40 sé'ahs are equal to 3 cubic ammahs, so 40 bats are equal to 9 cubic ammahs (see Biblical measuring units and Solomon's "Sea").
The kiyyors could have had many possible shapes. The simplest is a hemisphere, so let's consider that case first. The volume of a hemisphere of radius R is 2πR³/3 and if we put R = 2 ammahs (for a diameter of 4 ammahs), we find that the capacity will be almost 16.8 cubic ammahs, which is a lot more than the nine cubic ammahs (40 bats) specified by M'lachim Alef 7:38. The kiyyors therefore could not have been hemispheres.
It is possible to have a hemispherical kiyyor with a radius of 2 ammahs and a capacity of 9 cubic ammahs if we remove a spherical cap from the bottom so that the kiyyor has a flat base.
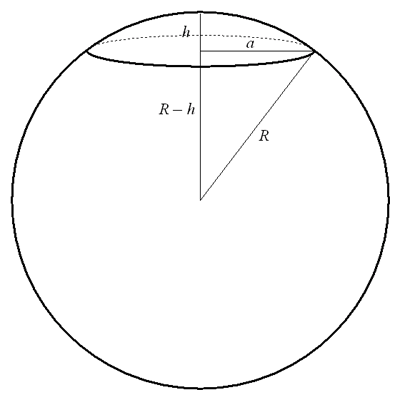 | 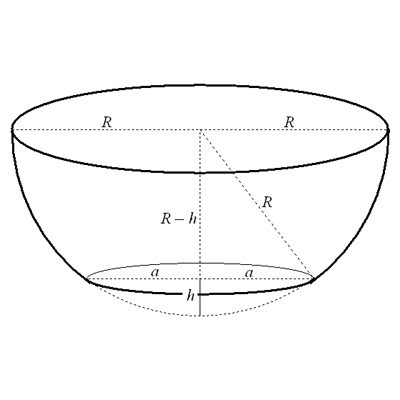 |
| Figure 2: "Cap" of a sphere | Figure 3: Kiyyor with flat circular base formed by removing a cap from a hemisphere |
Figure 2 illustrates a spherical "cap". A cap of a sphere is a portion of the sphere cut of by a plane that intersects the sphere. If the radius of the sphere is R, the height of the cap is h and the radius of the cap's base is a as shown in the diagram, the volume of the cap is given by
But since by Pythagoras's Theorem
we have
and so the volume of the "cap" can also be written as
For a more detailed explanation of spherical caps, see Eric W. Weisstein, "Spherical Cap", from MathWorld--A Wolfram Web Resource, http://mathworld.wolfram.com/SphericalCap.html.
So how big a cap do we have to remove from the two ammah radius hemisphere to get a basin with a capacity of nine cubic ammahs? The volume of the whole hemisphere is 2πR³/3 with R = 2, or 16π/3 (i.e. about 16.76 cubic ammahs), so we need to remove a cap of volume 16π/3 − 9 (or about 7.76 cubic ammahs). We therefore need to find a value of h that satisfies
with R = 2, i.e.
Multiplying every term by 3 and dividing by π simplifies this to
or
This is not the place for a detailed treatment of the solution of cubic equations. They are not easy beasts to solve (a very complicated algorithm for solving cubics is available online as Eric W. Weisstein, "Cubic Formula", from MathWorld--A Wolfram Web Resource, http://mathworld.wolfram.com/CubicFormula.html), and I have provided a simple program called cubic.exe for solving cubic equtions, that you can download if you wish. The program solves the equation ax³ + bx² + cx + d = 0, so to solve h³ − 6h² + (16 − 27/π) = 0 you need to supply the values a = 1, b = −6, c = 0 and d = 7.405633073. There are three solutions, namely h = −1.026616, h = 1.248424, and h = 5.778191, but the height of the "cap" must be positive, and cannot be greater than the radius R of the sphere (2 ammahs). It follows that the only possible value for the height h of the cap we will have to remove from the hemisphere is h ≈ 1.248, and the resulting basin will therefore be 2 − 1.248 ≈ 0.752 ammahs deep. The radius of the base can be calculated by using the relationship a² = 2hR − h², from which we find that a = (3.435134)½ ≈ 1.853 ammahs.
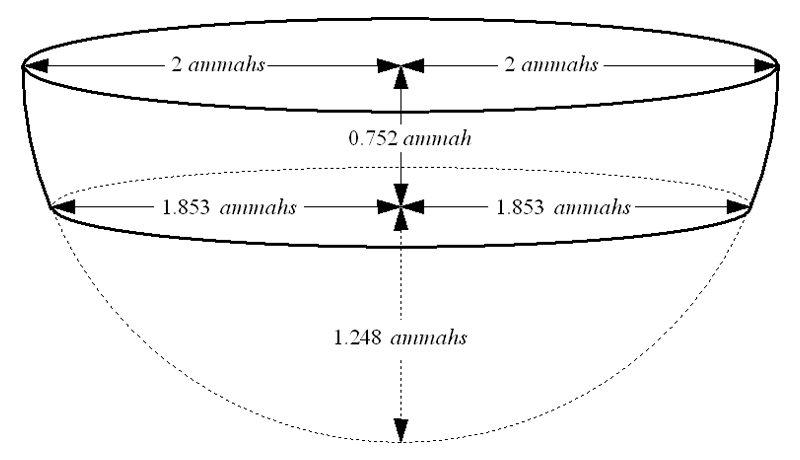 |
| Figure 4: Kiyyor consisting of a hemisphere of radius 2 ammahs with a cap of height 1.248 ammahs and radius 1.853 ammahs removed its capacity is 9 cubic ammahs or 40 bats |
If we were to cut caps of base radius a = 2 ammahs from larger and larger spheres, the volumes of the caps would get progressively smaller as the radius R of the sphere they are cut from increases. If we can find a value of h that satisfies
for a = 2, we will have a spherical cap 4 ammahs in diameter with a capacity of 9 cubic ammahs (i.e. forty bats), which would meet the specifications given in M'lachim Alef 7:38. This equation can be simplified and rearranged as
and putting a = 2 gives
or
This cubic equation has only one real root, occurring at h = 1.2640742. Now we found earlier that the relationship between the radius a and height h of a spherical cap and the radius R of the sphere it was cut from is
so that
and it follows that our spherical cap of radius 2 ammahs and depth 1.2640742 ammahs is cut from a sphere of radius 2.2142227 ammahs.
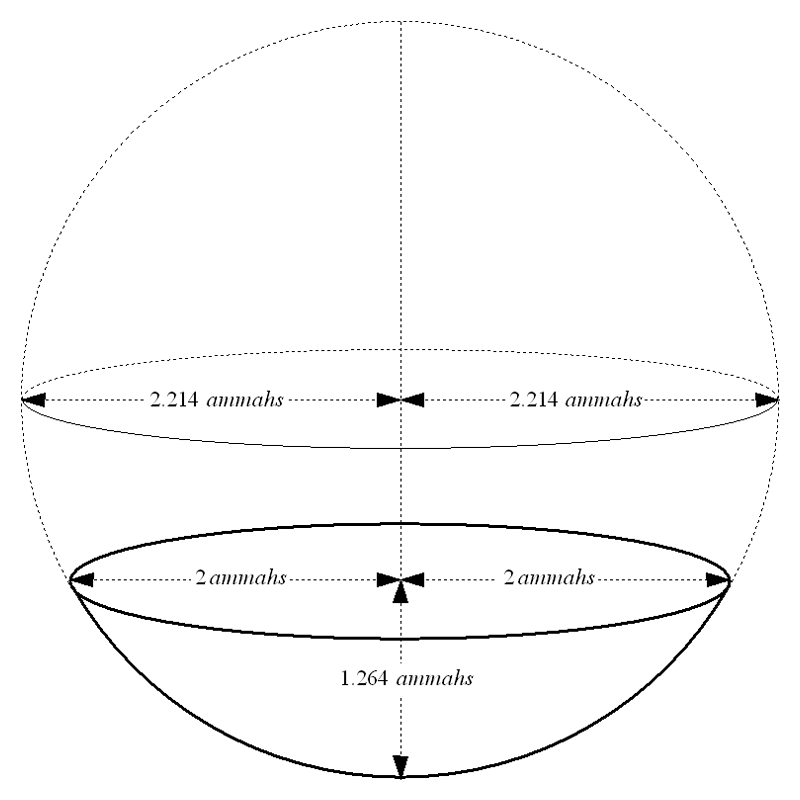 |
| Figure 5: Kiyyor consisting of a cap of a sphere... capacity 9 cubic ammahs or 40 bats |
In fact, we could make a kiyyor that holds 40 bats of water from a sphere with any radius between 2.000 ammahs and 2.214 ammahs by cutting a spherical cap with a base radius of 2 ammahs from the sphere and then removing a smaller spherical cap from the bottom to leave a flat base, just as we did with the hemisphere. The sphere we cut our cap from must have a radius of at least two ammahs because a spherical cap's base radius can't be greater than the sphere's radius, and it cannot be larger than 2.214 ammahs in radius or the kiyyor will not hold 40 bats of water.
I have spent a great deal of time discussing kiyyors made in the shape of parts of spheres, but there is nothing in the text to suggest that they were spherical. Could they have been conical? The volume of a circular cone is πr²h/3, where r is the radius of the cone's circular base and h is its vertical height (or, in this case, the depth of the conical kiyyor). Thus, 4πh/3 = 9, or h = 27/4π ≈ 2.149 ammahs. A conical kiyyor sitting on top of its m'chonah might have looked something like Figure 6:
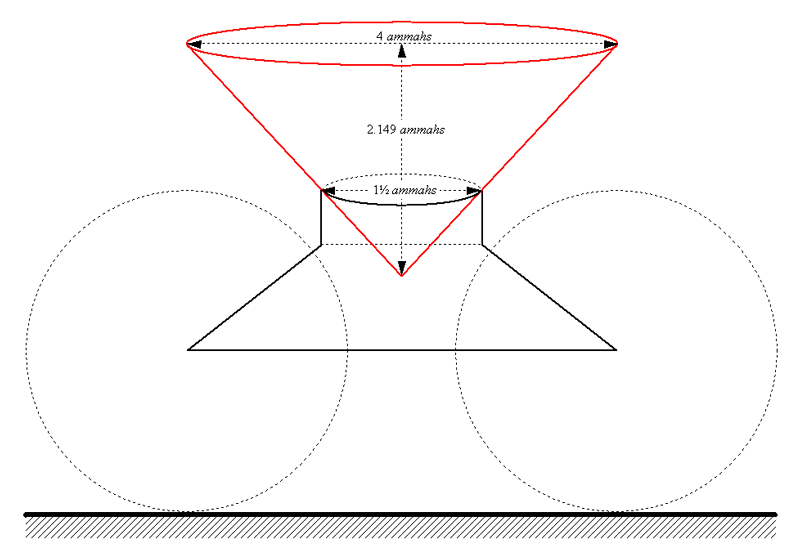 |
| Figure 6: Conical kiyyor on its m'chonah |
But that isn't the end of the story. We could also make a conical kiyyor four ammahs across that holds forty bats of water by taking a taller cone and chopping off the pointed end... a solid formed in this way is called a conical frustum, and is illustrated in Figure 7.
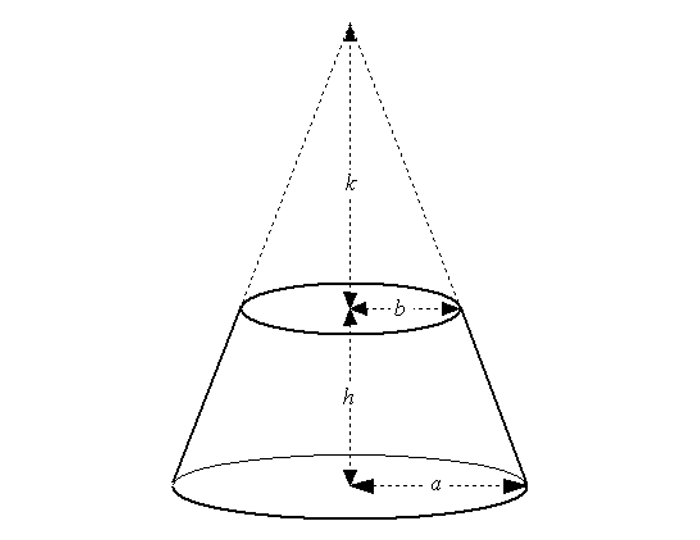 |
| Figure 7: Frustum of a circular cone |
In the diagram, a cone of height k has been chopped off the top of a larger cone, leaving a frustum of height h: the height of the original cone was thus h + k. If the radius of the original cone's base was a and the base-radius of the cone that we chopped off it to form the frustum was b, the radii of the frustum's two circular faces will therefore be a and b.
The volume of the original cone was 1/3πa²(h + k), and the volume of the cone we chopped off it is 1/3πb²k, so it follows that the volume of the frustum is
But it is apparent from consideration of the similar triangles in Figure 7 that
| a | = | b | |
| h + k | k |
so that
and so we can replace (a − b)k by bh and the expression for the volume of the frustum becomes
If we want to make a kiyyor in the form of a conical frustum, with a brim-diameter of four ammahs and a capacity of forty bats (i.e. nine cubic ammahs), the radius r of the base and the depth h of the kiyyor will have to satisfy
that is
or
This quadratic equation has roots given by
| r = ½{−2 ± √ | 4 − 4(4 − 27/πh) | } |
| r = −1 ± √ | 1 − (4 − 27/πh) |
| r = +√ | 1 − (4 − 27/πh) | − 1 | (choosing the positive value of the square root because r must be positive) |
| r = √ | 27/πh − 3 | − 1, |
which will be a real number if and only if the quantity under the square root sign is positive or zero... that is to say, if and only if
| 27 | ≥ 3 | πh |
or
However, the greatest possible value of h is even smaller than 2.865 ammahs, because r must be positive, so we must have
| √ | 27/πh − 3 | ≥ 1 |
or
so that
i.e.
There is also a smallest possible value of h, because r must be less than 2, the radius of the kiyyor's brim. Thus,
| √ | 27/πh − 3 | − 1 < 2 |
or
| √ | 27/πh − 3 | < 3 |
so that
| 27 | − 3 < 9 | πh |
i.e.
| 27 | < 12 | πh |
and finally
Furthermore, if the lowest part of the conical frustum is to fit inside the supporting cylinder on the top of the m'chonah, which has a diameter of 1½ ammahs, then r must be less than ¾ and we have
| √ | 27/πh − 3 | − 1 < 0.75 |
or
| √ | 27/πh − 3 | < 1.75 |
so that
| 27 | − 3 < 1.75² = 3.0625 | πh |
i.e.
| 27 | < 6.0625 | πh |
and finally
Consequently, to meet the specifications stated in M'lachim Alef 7:38, a kiyyor made in the form of a conical frustum would need to have a depth h between 1.418 ammahs and 2.149 ammahs and related to its base radius r by
| r = √ | 27/πh − 3 | − 1 |
which is equivalent to
| h = | 27 | |
| (r² + 2r + 4)π |
The relationship between h and r is shown by the graph in Figure 8:
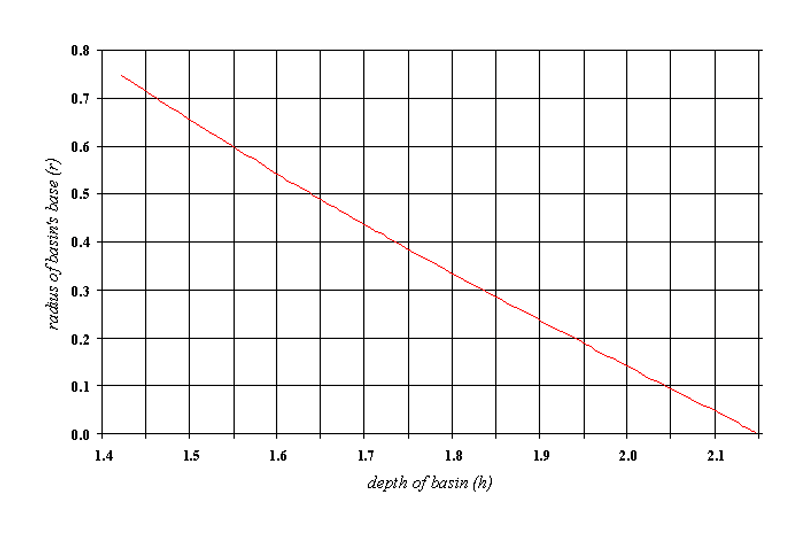 |
| Figure 8: Relationship between h and r for a kiyyor made in the form of a conical frustum |
Any advertisements appearing below this line are inserted by "tripod", please IGNORE them